|
||||
|
Self-organized middle-out abstraction of complexity
| Permalink Today, the inherent complexity of many man-made or naturally occurring challenges—such as understanding the influence of human interference in ecosystems or interacting biological processes—is widely acknowledged. The ubiquitous networking paradigm has highlighted the elaborate webs of interactions and interdependencies between living beings, objects and processes. Yet we still lack an algorithmic framework capable of tackling the complexity of the world, in terms of representation and computation. Thus, any step towards understanding—and perhaps even predicting—the dynamics and emergent phase transitions of complex systems would greatly contribute to the advancement of science. 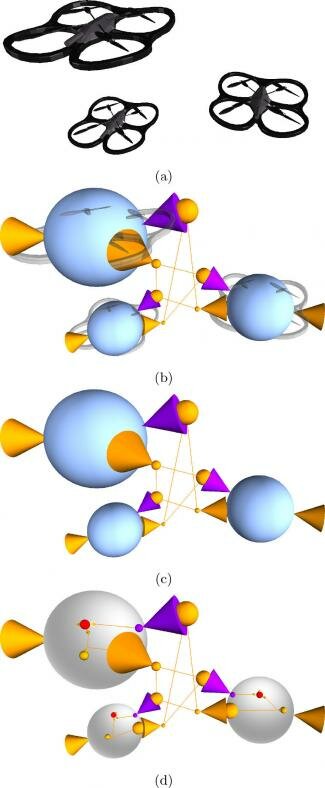Figure 1. (a) Three quad-copter agents situated closely together. (b) Projection of the agents' behavioural operators and their interrelations into the agent space. (c) Focus on the behavioural network. (d) Introspection of the agents' behavioural modules reveals hierarchically nested, lower-level operators and their connectivity. 
Present-day societal challenges that could benefit from this kind of knowledge are plentiful, and can be found in fields ranging from the life sciences to economics and engineering. To some extent, the mathematical analysis of complex systems can provide some insights about the phase transitions that may occur over time.1, 2 However, this approach requires a great deal of effort and does not scale well, becoming intractable as the number of factors involved in a system increases. What is more, the interactions that drive system transitions must be identified and formalized a priori by the modeller. In contrast, an ideal model building process should require as little information as possible about a system's actual behaviour. It should be enough to only describe how the parts of a system interact, without building in any assumptions about when feedback cycles might be triggered and snowball into fundamental global system changes. In a model of this kind, the parts of the system that interact according to sets of internal rules (and so without any external, higher-level drivers of their collective behaviour) are known as ‘agents’. Each agent in such a model is thus a self-contained entity with its own individually accessible data, states and behaviours, often expressed in the form of ‘if-then’ rules. The interaction sequences among agents and the traversal of their states in a computational simulation correspond to the emergent feedback cycles and phase transitions of complex systems. If we were able to detect patterns that are precursors to phase transitions and patterns that correspond to the system's global dynamics, we could automatically become aware of emergent phenomena. To pursue this goal, in early 2011 we presented the design of the self-organized middle-out (SOMO) concept,3 an approach for automatic adaptive abstraction that is neither top-down nor bottom-up, but instead operates at an intermediate, or ‘meso’, level of analysis. Its foundation is an unsupervised learning method that observes and abstracts processes which occur (that is to say, emerge) during a computational simulation. An abstracted process is no longer executed, but whenever its preconditions hold, its observed side effects are enacted in the system. Such automatically abstracted process descriptions promise to help us understand, explain and compute complex phenomena in simple terms. SOMO observes the simulation data and identifies process patterns, ‘biased’ only in terms of its representations (meaning that the way interaction patterns are represented by SOMO can influence the kinds of patterns that can be detected and so bias the result). The patterns identified in this way are used to refine the computational model that drives the simulation process being observed. As the SOMO algorithm continues to observe and learn the patterns that emerge from the simulation, it continually increases the level of abstraction by introducing hierarchies of abstracted patterns. It is hoped that such hierarchies will to some extent coincide with the real-world conceptual boundaries that we identify in natural systems, such as the subdivision of the organizational complexity of animal anatomy into cells, tissues and organs. Since such abstractions are inevitably subject to noise and unknown conditions, we also introduce a confidence measure that is associated with each abstraction. Figure 1 shows a visualization of the behaviours and interrelations of a set of interacting agents. The individual operators (agents), represented by spheres, are recursively nested to allow for the hierarchical design of behavioural modules, while the connections between inputs and outputs, represented by cones, determine the flow of information at each hierarchical level.4 The creation of this visual modelling language was in part motivated by the need for a generic, hierarchical representation of agent behaviours. We envisage that a SOMO agent designed along these lines could eventually be exposed to an arbitrary multi-agent simulation, and be capable of automatically inferring hierarchies of patterns from the processes which it observes. Accomplishing such a universal deployment of the SOMO concept would require, among other things, a generic learning mechanism for identifying arbitrary patterns,5 a universal approach to measuring and comparing confidence values6 and a reinforcement learning mechanism,7 as well as a comprehensive formalization of representation and algorithms. It has already been shown that current implementations of SOMO are capable of pruning computational complexity in multi-agent-based simulations and identifying emergent processes.8–13 A broadly deployable, unbiased SOMO implementation would make it possible to compute models with large numbers of approximate constants, such as in our perceived reality. This would make it possible to integrate vast quantities of scientific facts, across all levels of scale and scientific disciplines, for consideration in simulations. What is more, the SOMO concept need not be limited to virtual simulations. It could also operate on top of a smart sensory network to form a ‘SOMO net’. Adding sensory nodes with effectors would introduce the further capability of self-directed inquiry. At that point, the SOMO net would turn into a self-reflective machinery similar to the one developed by Lipson et al.,14 which also acquired the converse capability of automatically inferring complex, non-linear mathematical laws from data sets by avoiding trivial invariants.15 A SOMO net enhanced in this way would be able to autonomously perform observational analysis and pro-active investigations to further accelerate the generation of comprehensive and accurate scientific models. In summary, the SOMO algorithm and SOMO nets hold the promise of revealing hitherto unsuspected correlations between processes. Such new insights, and the immense complexity that SOMO can handle, would help to build the sustainable, progressive and evolving economic and ecological infrastructures for tackling the major challenges humankind faces today. Our current work on SOMO is focused on pattern detection in observed interactions and the possibilities for propagating knowledge about abstractions through the system. Once the implementations of SOMO have reached maturity, we envisage that research can shift to analysing how the learned abstractions and features correlate with the behaviours we find in higher-order emergent phenomena. Whether we will find striking similarities, or instead discover these to be two completely different forms of complex systems, remains an exciting open question at this time. References
Stay Informed
|
||||
|
||||